lobibro.blogg.se - Circle iunit

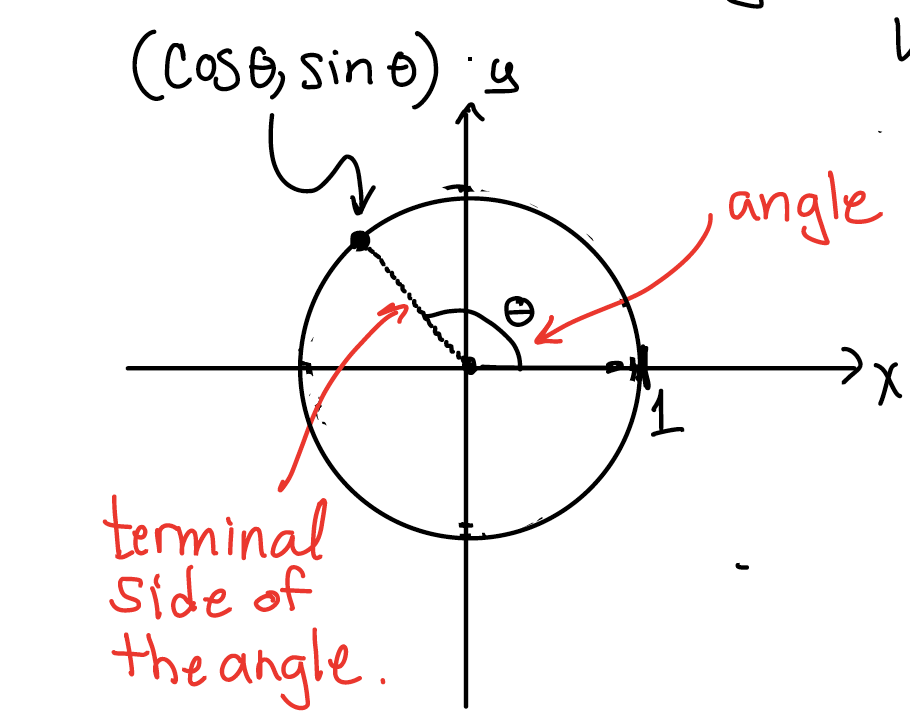
In unit circle, tangent is not usually present, instead just cos and sin values are present. So divide the y-coordinate by the x-coordinate of each point on the unit circle to find the corresponding tangent value. We have an identity tan x = (sin x) / (cos x). We already have cos and sin values on the unit circle where each point on the unit circle gives the coordinates (cos, sin). Tan is negative in 2 nd and 4 th quadrants.įAQs on Unit Circle With Tangent How do You Find Unit Circle With Tangent?

Tan is positive in 1 st and 3 rd quadrants and.

The tan values on unit circle are symmetric with respect to both the axes except for the signs.

Tangent is NOT defined only at π/2 and 3π/2 on the unit circle.

Important Points on Unit Circle With Tangent: Here is the graph of the tangent function using the unit circle. While plotting the points, let us use the following decimal approximations: Let us just use the "unit circle with tangent chart" to plot the points and join them by curves taking care of the vertical asymptotes.

Let us plot the x-axis with the angles from 0 to 2π with the intervals of π/4 and y-axis with real numbers. So we get vertical asymptotes at x = π/2 and at x = 3π/2 in the graph of tangent function. Thus, the unit circle with tangent chart is as follows:įrom the unit circle with tangent, we can clearly see that tan is NOT defined for the angles π/2 and 3π/2.

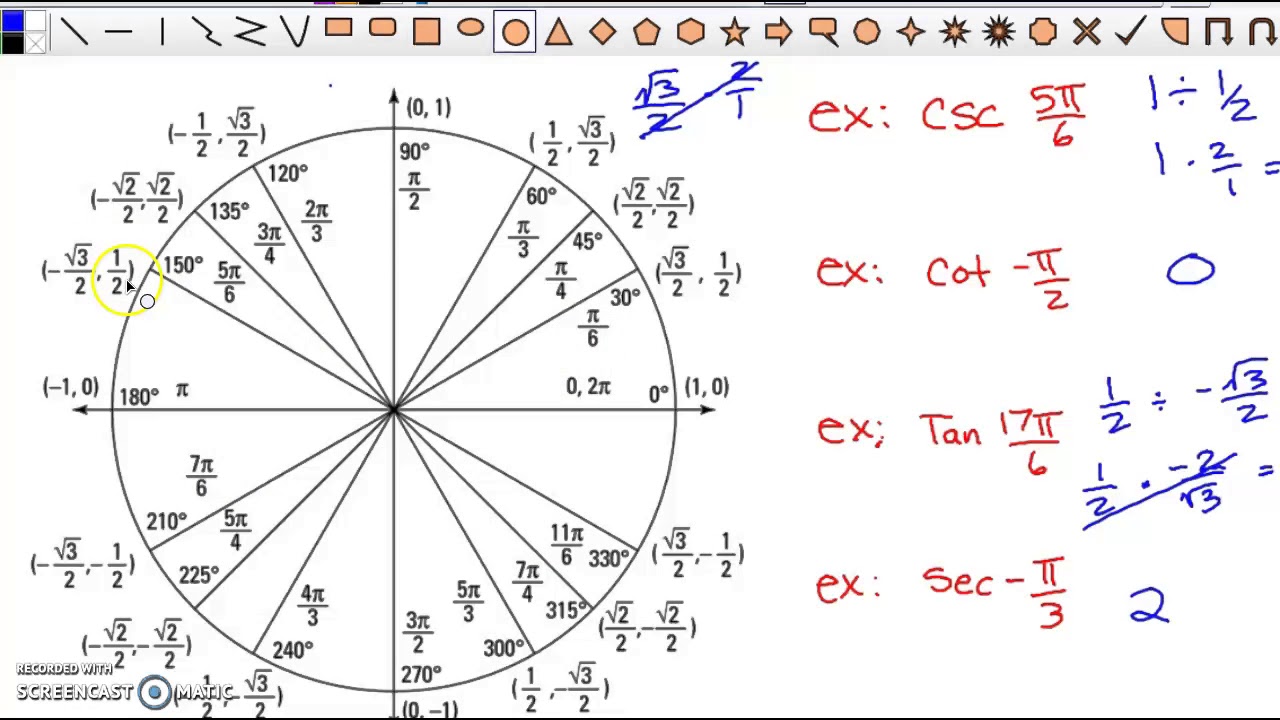
Now, we will use the identity tan x = (sin x)/(cos x) in each row to compute the corresponding value of tangent. To compute the value of tangent, let us recall the values of sin and cos at the standard angles from 0 to 2π.